我要带朋友们潜入水下参观密码学的一些技术概貌。当然我们不可能把每个细节都搞清楚,我们仅深入到能够理解区块链技术原理的深度就返航(再深入会掉粉的)。再次提醒朋友们,区块链技术有现在的气质靠的是密码学,梦想创新创业的,建议深入了解密码学,然后用这个技术去比划各种行业,也许会有海阔天空的感觉。
未来这几期,我想介绍密码技术里最基础的两个,分别是散列函数和数字签名。这两个技术应用范围非常广,我们日常工作生活中已经有相当多的应用了,只是我们很多人并没有感受到。
先说散列函数。技术小白请不要吐槽,更不要退订我的公众号,尽管“散列函数”的名称不论听和看都不那么友好,其他的名字像什么“哈希函数”、”杂凑函数”也差不多德性,英文叫HASH还算简洁,它还有一个比喻称呼叫“数字指纹”,算是有点亲民了。
在计算机出现以前,人们就对文章书籍有提取摘要信息和关键词的需求,目的是为了提高查阅、检索的速度。计算机出现以后,由于计算机处理数据时最重要的工作之一就是检索,如何提高计算机的检索效率是提高计算机处理数据能力的重要指标。显然计算机检索数据的方式与人们翻阅图书馆信息检索卡片不一样,计算机有自己的语言和阅读方式,因此设计如何获取好用的信息摘要是一门看家手艺。

图示:大英图书馆纸质卡片目录
现代密码学以信息论、数学为依托,研究的主要目标就是如何处理信息并安全的传递。网上传递的各种各样信息,在网络的底层都是变成二进制数字在铜线里、空中电波中传递,如何让接收方校验发送方发来的数据是完整正确的?从数字通信应用开始之前,这个校验问题就必须解决掉。
专家们发明了许多校验技术。例如“校验和”(checksum),这种校验方式非常简单,就是发送方把传输的二进制数字按位加起来,例如要传输“0101101”这个数字串,就把里面4个1加起来,然后把结果数(例子的和为4)和原始数字串(要传递的信息“0101101”)传给接收方,接收方自己也把收到的信息加起来,比较与收到的“和”一样不一样,来确定是不是收对了。聪明的小白们看完一定一脑袋问号,这种校验也太粗糙了吧,原来技术世界的精细活也不是那么高深呀?
随着研究越来越深入,高深的散列函数出现了,它实在太有用了,被称为密码学的瑞士军刀。有了前面问题需求的铺垫,我现在可以直接介绍散列函数是干什么的。说白了(技术小白的白),散列函数就是把一段无论多长的数据串(可以是文字、文章、电影、音乐)转换成一个固定长度的数值,这个数值就是一个数字,计算机里面存的是二进制,一般显示给我们看的是16进制。而这个固定长度一般是指在二进制下的固定位数。
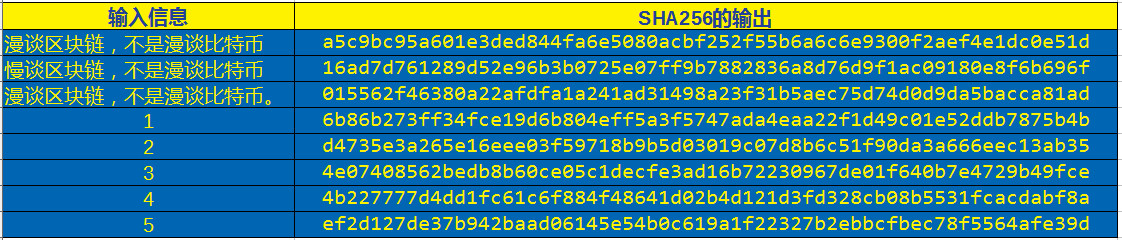
图示:散列函数被输入不同信息,哪怕非常小的差别,输出都是完全不一样的结果(SHA256是比特币中使用的散列函数)
如今散列函数有许多应用,我们网上下载文件是不是完整的校验就是靠它实现的。现在手机音乐都有“听歌识曲”功能,不了解原理的人一定很好奇,机器怎么做到这么智能的识别音乐呀?其实音乐歌曲都是数字方式存储的,对散列函数来说就是一串二进制数字,可以计算其中一段或者整首歌的散列值作为索引。那么手机在听歌的时候其实是在录制成数字音乐,再计算散列值并与歌曲库的散列值去对比查找,并不是手机也懂音乐了。
散列函数在比特币的技术架构主要用到三个方面的特性(还有许多其他特性,但不是比特币应用中所关注的,所以就不介绍了),本篇介绍碰撞阻力。
今天总是遇到这种每个字都认识,放在一起完全不知道啥意思的词,当然我会想尽办法让朋友们看明白的。这个特性的重要性直接关系到比特币的信任基础,上一篇我的副标题是信任的基石,是指整个密码学是比特币技术应用的信任之源,在密码学内,这个哈希函数的碰撞阻力可以说是基石的基石。
前面图示中我例举了几个输入,然后看看在SHA256算法的输出,我在图示中提到哪怕很接近的输入,都有不同的输出。一定有朋友会想,难道就不会出现不同信息输入,会有同样输出的情况吗?会的,如果出现这种情况,就叫出现了碰撞。碰撞阻力的意思就是很难找到碰撞,最好永远也找不到。这是一部分以加密为目标的散列函数的梦想。
但是理想归理想,现实很残酷,理论上人类是不可能找到这种完美算法的。为什么呢?我们拿上篇“生日悖论”的例子来说。
每个人生日就如同散列函数的结果一样,是有固定数量的,总共也就有365个可能性(不考虑闰年)。如果超出365人,有366个人,那么无论如何都会有两个人落在同一天过生日。这个也叫“鸽巢原理”、“抽屉原理”。
对于散列函数也是如此,SHA256这种算法的输出是256位二进制数字,也就是说总共就有2256个可能性,这个数字是很大,但也不是无限的呀。而我们可以选择的输入信息可是无限的可能性,最简单的就是我们可按1、2、3……不断输入来计算散列值,总有一天我们会输入到2256+1,那么就必然会出现两个输入产生了一个结果。
所以哈希函数完全杜绝碰撞是不可能的,可是数学家们不会因为不可能就不再去努力,因为可能性本身就是一门实用数学——概率论。既然完全杜绝是不可能的,那么能不能想办法让碰撞非常非常非常难发生呢?
有两个努力方向,首先是把算法研究的更加精深,这个咱就不介绍了(说的好像我能介绍似的,其实我根本不懂,但我相信世界上最聪明人的研究成果)。另外一个是增加固定输出的可能性数量,让尝试碰撞的努力变成天荒地老,海枯石烂的事情。
“生日悖论”的例子里,在365个可能性结果情况下,经过概率计算,需要23个人就能达到50%的碰撞可能性。同样的在2256个可能性结果情况下,数学家算出来达到50%碰撞可能性的尝试次数大约是2128次。这个数字有多大呢?
普林斯顿大学Arvind Narayanan, Joseph Bonneau, Edward Felten, Andrew Miller, Steven Goldfeder等四位教授编著的网络课程教材《Bitcoin and Cryptocurrency Technologies》里是这么说的:如果一台电脑每秒计算一万个散列值,需要计算1027年;换个角度,如果人类到今天为止制造的所有电脑,在整个宇宙起源的时刻(137亿年前)便开始计算,到今天能找到碰撞的概率仍然很小,比两秒后地球被大陨石摧毁的概率还要小得多。(在视频课程里,教授停了一下,然后说,两秒钟过去了,咱们还在。)
散列函数有很多,区别在于采用的计算方法和输出的长度有区别,目前流行的有MD5,SHA1、SHA2等等。我很反感用英文单词首字母组合表示一个东西,又不解释一下的行为,这是人为制造学术壁垒。其实这些组合看上去高大上,其实解开来非常简单容易记。每当我遇到大写字母组合,我就要去查查到底是哪个单词组成的,例如MD,其实就是Message-Digest Algorithm(信息摘要算法),看看多朴素。再例如SHA,其实就是Secure Hash Algorithm(安全哈希算法),同样的朴实无华。后面的数字是更新迭代的序号。
如果说设计散列函数是一批绝顶聪明的数学家制造“盾”的工作,那么还有一些绝顶聪明的科学家在做“矛”的事情。这些人仔细研究各种算法的细节,然后想尽办法去找出碰撞的机会。正是这样的研究,让散列函数在现实应用中能保证其安全性。
山东大学的密码学专家,中国科学院院士王小云教授在这个领域有杰出贡献。2004年的国际密码讨论年会(CRYPTO)尾声,王小云及其研究同事展示了MD5、SHA-0及其他相关散列函数的散列冲撞。

图示:王小云教授(百度图片搜的)
2005年2月,王小云与其同事提出SHA-1散列函数的散列冲撞。由于SHA-1散列函数被广泛应用于现今的主流计算机安全产品,其影响可想而知。SHA-1输出的是160位长度的散列值,也就是说有2160个可能性,按照“生日悖论”所用计算的概率方法计算,理论上达到50%的碰撞可能性需要尝试280次,王小云所提的散列冲撞算法只需少于269次。同年8月,王小云、姚期智,以及姚期智妻子姚储枫联手,于国际密码讨论年会提出SHA-1散列函数散列冲撞算法的改良版,缩短为少于263次。
看到263次方这个数字,我脑袋里闪出小时候听过的故事,一个人向国王要奖赏,在国际象棋棋盘上,第一个格子放一粒米,第二个放2粒,第三个4粒,第四个16粒…..直到最后一个格子是264粒米的故事。看来263次好像也是天文数字呀。
目前公认最安全的是SHA-2家族,比特币采用的是SHA2家族中输出长度为256的算法,也被称之为SHA256。此外,SHA-3 相关算法也已被提出。
许多朋友心中有一句广告词——“一切皆有可能”,而这句话对散列函数防止碰撞能力一定是存疑的,总担心万一碰巧哪一天发现了碰撞呢。然而数学告诉我们“一切皆有概率”,相信数学,就信散列函数。如果建立不了这个信任,现实世界不仅仅是比特币,许多应用都将在你的心目中不再可靠,只是以前你不知道罢了。
好了,先结束这篇吧,其他两个散列函数的特性放到下一篇继续……
(本篇首发于2018年3月12日微信公众号geekszone)